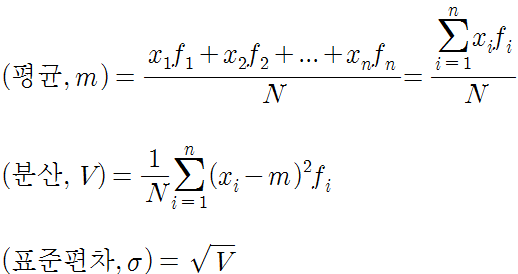안녕하세요 반갑습니다. 즐거운 화요일이 이렇게 다가왔습니다 항상 도움이 되기 위한 조건과 노력으로 저희는 불안이나 걱정이 없도록 상황을 판단하고 그에 따른 합리적인 제안과 구성을 하고 있습니다.어려운 상황이 발생하지 않도록 올바른 광고기획과 더불어 합리적인 선택과 계좌확보까지 고려하여 상담하고 있습니다. 상세한 처리와 마무리까지 어떤 형태로 솔루션과 기획을 하면 더 나은 조건의 광고송출이 가능한지에 대해 논의하고 있습니다. 오늘은 본론으로 돌아와 업무이야기로 내용을 함께 다루고자 하는 주제는 표준편차통계표본수학 공식입수에 관한 것입니다.
우리는 생활 속에서 다양한 형태의 수학교육과정을 받게 됩니다. 학년별, 그리고 난이도별로 그에 따른 선행학습으로 미리 교육을 받고 있는 것은 예나 지금이나 계속 같다고 할 수 있는 수학에 관심이 있는 사람도 있는 반면 수학에 흥미를 갖고 있거나 그에 따른 가치를 얻는 데 많은 사람들이 관심을 가지고 있습니다. V(X) = E(x제곱)-{E(X)}제곱 분산 제곱의 평균 제곱

그렇게 수학의 표준편차를 구하는 방법에 대해 새롭게 접하거나 혹은 예전에 배운 공식에 대해 다시 한번 되새기기 위해 찾아보는 것이 아닐까 생각합니다.
먼저 편차를 구하려면 먼저 평균값을 알아봐야 합니다. 예를 들어, 제가 원하는 평균값을 판단해야 합니다. 철수가 다니는 반은 모두 4학급으로 되어 있습니다. 그 반에서 받은 수학 점수에 대한 모든 값을 평균해야 합니다. 이렇게 분산을 적용시키고, 그에 대한 변량의 개수에 맞게 편차에 곱하기 2를 해주신 담녀, 그에 따른 값이 나옵니다.

이러한 통계자료는 말 그대로 표준에 따라 어떤 편차, 즉 차이가 있는지를 보여주는 통계라고 할 수 있습니다. 평균에서 벗어나는 근사치의 값을 구할 수 있습니다. 이러한 적용은 과거사를 통해 미래를 예측할 수 있기 때문에 더 많은 분들이 관심을 가지고 있는 부분이라고 할 수 있습니다. 공식으로 돌아왔을 때 평균값을 구하고 분산되어 서양 제곱근을 추가로 넣음으로써 표준편차가 발생합니다.

먼저 수학의 기본 적용은 기본 공식 틀에서 크게 벗어나지 않기 때문에 수식이나 내용이나 이를 어떻게 적용하느냐에 따라 그 값이 달라지는 것입니다.

표준편차는 우선 이렇게 쉽고 간단하게 구할 수 있습니다. 다음에도 더 유익한 팁과 다양한 정보로 인사드리겠습니다!^^ 남은 하루 즐겁게 채워가시길 바라며 오늘의 이야기를 마치도록 하겠습니다

#표준편차 구하는법 #분산공식 #수학공식을 구하다